Featured Post

List of Questions and link to solutions

Chapter 1: Vector Analysis Problem 1.1: Using the definitions in Eqs. 1.1 and 1.4, and appropriate diagrams, show that the dot product and cross product are distributive, a) when the three vectors are co-planar. b) in the general case.  Solution   Problem 1.2 Is the cross product associative? $$(\vec{A}\times \vec{B}) \times \vec{C} \overset{?}{=} \vec{A}\times (\vec{B} \times \vec{C})$$ If so, prove it; if not, provide a counterexample (the simpler the better). Solution   Problem 1.3 Find the angle between the body diagonals of a cube.  Solution Problem 1.4 Use the cross product to find the components of the unit vector $\hat{n}$ perpendicular to the shaded plane in Fig. 1.11. Solution   Problem 1.5 Prove the BAC-CAB rule by writing out both sides in component form. Solution Problem 1.6 Prove that $$[\vec{A}\times (\vec{B}\times \vec{C})]+[\vec{B}\times (\vec{C}\times \vec{A})]+[\vec{C}\times (\vec{A}\times \vec{B})] = 0$$ Under what conditions does $\vec{A}...
2 comments

Chapter 1 Vector Analysis: Problem 1.1

Problem 1.1: Using the definitions in Eqs. 1.1 and 1.4, and appropriate diagrams,
show that the dot product and cross product are distributive,
a) when the three vectors are co-planar.

b) in the general case.

Solution: 

Eq$^n$ 1.1

$$\vec{A}\cdot \vec{B} = |A||B| \cos\theta$$where $\theta$ is the angle between the vectors $\vec{A}$ and $\vec{B}$

Eq$^n$ 1.4

$$\vec{A}\times \vec{B} = |A||B| \sin\theta \hat{n}$$where $\theta$ is the angle between the vectors $\vec{A}$ and $\vec{B}$, and $\hat{n}$ is a unit vector normal to both $\vec{A}$ and $\vec{B}$.

We have to show that:

$$\vec{A}\cdot (\vec{B}+\vec{C}) = \vec{A}\cdot \vec{B}+\vec{A}\cdot \vec{C}$$

$$\vec{A}\times (\vec{B}+\vec{C}) = \vec{A}\times \vec{B}+\vec{A}\times \vec{C}$$

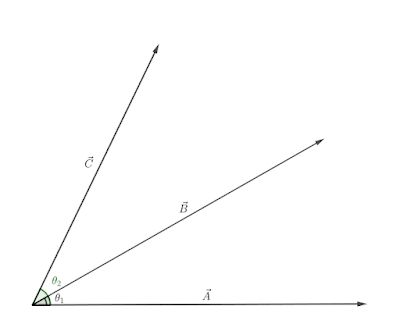
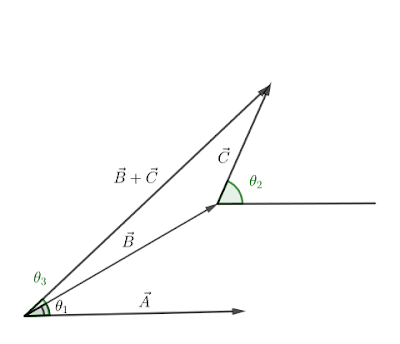
$a) $ When $\vec{A}$, $\vec{B}$ and $\vec{C}$ are co-planar. 


$\theta_1$ and $\theta_2$ are the angles the vector $\vec{B}$ and $\vec{C}$ makes with the $\vec{A}$ respectively.

To get $\vec{B}+\vec{C}$ put the tail of $\vec{C}$ on the head of $\vec{B}$.

 



Let $\theta_3$ be the angle the resultant $\vec{B}+\vec{C}$ makes with the $\vec{A}$.

Draw the components of $\vec{B}, \vec{C}$ and $\vec{B}+\vec{C}$ along $\vec{A}$.



$$\therefore |\vec{B}+\vec{C}|\cos\theta_3 = |\vec{B}|\cos\theta_1+|\vec{C}|\cos\theta_2$$
 
Multiplying both sides by $|A|$
 
$$\therefore |A||\vec{B}+\vec{C}|\cos\theta_3 = |A||\vec{B}|\cos\theta_1+|A||\vec{C}|\cos\theta_2$$
 
From eq$^n$ 1.1 this is nothing but,
 
$$\vec{A}\cdot (\vec{B}+\vec{C}) = \vec{A}\cdot\vec{B}+\vec{A}\cdot\vec{C}$$

In the same way, take components along the normal to the vector $\vec{A}$.
 
$$\therefore |\vec{B}+\vec{C}|\sin\theta_3 = |\vec{B}|\sin\theta_1+|\vec{C}|\sin\theta_2$$
 
Multiplying both sides by $|A|\hat{n}$
 
where $\hat{n}$  is the vector normal to the plane containing the vectors $\vec{A}, \vec{B}$ and $\vec{C}$.
 
$$\therefore |A||\vec{B}+\vec{C}|\sin\theta_3\hat{n} = |A||\vec{B}|\sin\theta_1\hat{n}+|A||\vec{C}|\sin\theta_2\hat{n}$$
 

From eq$^n$ 1.4 this is nothing but,

$$\vec{A}\times (\vec{B}+\vec{C}) = \vec{A}\times\vec{B}+\vec{A}\times\vec{C}$$

$b) $ For the general case.

As suggested by the author of the book, you should read the corresponding proof in the book G.E Hay' Vector and Tensor Analysis. Link to the book: http://bayanbox.ir/view/7717647651178235179/Hay-Vector-and-Tensor-Analysis.pdf

Consider

$\vec{A} = A_x\hat{i}+A_y\hat{j}+A_z\hat{k}$, $\vec{B} = B_x\hat{i}+B_y\hat{j}+B_z\hat{k}$, and $\vec{C} = C_x\hat{i}+C_y\hat{j}+C_z\hat{k}$

 Scalar product of two vectors is given by

$$\vec{A}\cdot \vec{B} = A_xB_x+A_yB_y+A_zB_z$$

 

$$\vec{A}\cdot (\vec{B}+\vec{C}) = (A_x\hat{i}+A_y\hat{j}+A_z\hat{k})\cdot ((B_x\hat{i}+B_y\hat{j}+B_z\hat{k}) + (C_x\hat{i}+C_y\hat{j}+C_z\hat{k}) )$$

$$\vec{A}\cdot (\vec{B}+\vec{C}) = (A_x\hat{i}+A_y\hat{j}+A_z\hat{k})\cdot ((B_x+C_x)\hat{i}+(B_y+C_y)\hat{j}+(B_z+C_z)\hat{k})$$

$$\vec{A}\cdot (\vec{B}+\vec{C}) = A_x(B_x+C_x)+A_y(B_y+C_y)+A_z(B_z+C_z)$$

$$\vec{A}\cdot (\vec{B}+\vec{C}) = A_xB_x+A_yB_y+A_zB_z+A_xC_x+A_yC_y+A_zC_z$$

$$\vec{A}\cdot (\vec{B}+\vec{C}) = \vec{A}\cdot \vec{B}+\vec{A}\cdot\vec{C}$$


Vector Product of two vectors is given by:

$$\vec{A}\times \vec{B} = \begin{vmatrix}\hat{i} & \hat{j} & \hat{k}\\ A_x & A_y & A_z \\ B_x & B_y & B_z\\ \end{vmatrix}$$

Consider

$$\vec{A}\times (\vec{B}+\vec{C}) = (A_x\hat{i}+A_y\hat{j}+A_z\hat{k})\times ((B_x+C_x)\hat{i}+(B_y+C_y)\hat{j}+(B_z+C_z)\hat{k})$$

$$\vec{A}\times (\vec{B}+\vec{C}) =\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z \\ (B_x+C_x) & (B_y+C_y) & (B_z+C_z)\end{vmatrix}$$

Using the property of addition of determinants:

$$\vec{A}\times (\vec{B}+\vec{C}) =\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z \\ B_x & B_y& B_z \end{vmatrix} + \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z \\ C_x & C_y& C_z \end{vmatrix} $$

$$\vec{A}\times (\vec{B}+\vec{C}) = \vec{A}\times \vec{B} + \vec{A}\times \vec{C}$$

 Hence, proved.


If you have any doubt regarding the solution or you want solution of some problem which is not posted please let me know by commenting. This encourages me to answer more question because sometime it feels like all I am doing is just a waste. If it helps someone I will be happy to do it.

 

If you have any doubt regarding the solution or you want solution of some problem which is not posted please let me know by commenting. This encourages me to answer more question because sometime it feels like all I am doing is just a waste. If it helps someone I will be happy to do it.

Comments

Post a Comment

Popular posts from this blog

Chapter 1 Vector Analysis: Problem 1.12

Image
Problem 1.12 The height of a certain hill (in feet) is given by $$h(x, y) = 10(2xy − 3x^2 − 4y^2 − 18x + 28y + 12),$$ where $y$ is the distance (in miles) north, $x$ the distance east of South Hadley. (a) Where is the top of the hill located? (b) How high is the hill? (c) How steep is the slope (in feet per mile) at a point 1 mile north and one mile east of South Hadley? In what direction is the slope steepest, at that point? Solution: Before proceeding to the answer, I strongly encourage you to watch this amazing video to get better insight of gradient:  https://youtu.be/QQPz3eXXgQI OR if you are something who wants to learn by reading here's a great article  https://betterexplained.com/articles/vector-calculus-understanding-the-gradient/ . I hope you must have watched or/and read the article before proceeding. $$h(x,y) = 10(2xy-3x^2-4y^2-18x+28y+12)$$ First let's compute gradient of the function: $$\vec{\nabla} h = \frac{\partial h}{\partial x}\hat{i}+\frac{\partial h}{\pa...
Read more

List of Questions and link to solutions

Image
Chapter 1: Vector Analysis Problem 1.1: Using the definitions in Eqs. 1.1 and 1.4, and appropriate diagrams, show that the dot product and cross product are distributive, a) when the three vectors are co-planar. b) in the general case.  Solution   Problem 1.2 Is the cross product associative? $$(\vec{A}\times \vec{B}) \times \vec{C} \overset{?}{=} \vec{A}\times (\vec{B} \times \vec{C})$$ If so, prove it; if not, provide a counterexample (the simpler the better). Solution   Problem 1.3 Find the angle between the body diagonals of a cube.  Solution Problem 1.4 Use the cross product to find the components of the unit vector $\hat{n}$ perpendicular to the shaded plane in Fig. 1.11. Solution   Problem 1.5 Prove the BAC-CAB rule by writing out both sides in component form. Solution Problem 1.6 Prove that $$[\vec{A}\times (\vec{B}\times \vec{C})]+[\vec{B}\times (\vec{C}\times \vec{A})]+[\vec{C}\times (\vec{A}\times \vec{B})] = 0$$ Under what conditions does $\vec{A}...
Read more

Chapter 1 Vector Analysis: Problem 1.16

Image
Problem 1.16 Sketch the vector function $$\vec{v} = \frac{\hat{r}}{r^2}$$ and compute its divergence. The answer may surprise you.. can you explain it? Solution:  Let's first sketch the given vector function. NOTE: Use this site to sketch vector function and play with it: https://c3d.libretexts.org/CalcPlot3D/index.html   Since it seems too complicated, let's see it from the top and see the field on the $x-y$ axis Now as we can see there is a net outward flux at the origin since the field is generated from the origin. So divergence at origin should be some positive value. We can't say anything about other coordinates as the field is expanding out but at the same time the magnitude is decreasing. Now compute the divergence:   $$\vec{v} = \frac{\hat{r}}{r^2}$$ $$\vec{\nabla}\cdot \vec{v} = \frac{1}{r^2\sin\theta}\big[\frac{\partial}{\partial r}(r^2\sin\theta v_r)+\frac{\partial}{\partial \theta}(r\sin\theta v_{\theta})+\frac{\partial}{\partial \phi}(rv_{\phi})\big]$$ $$\vec...
Read more