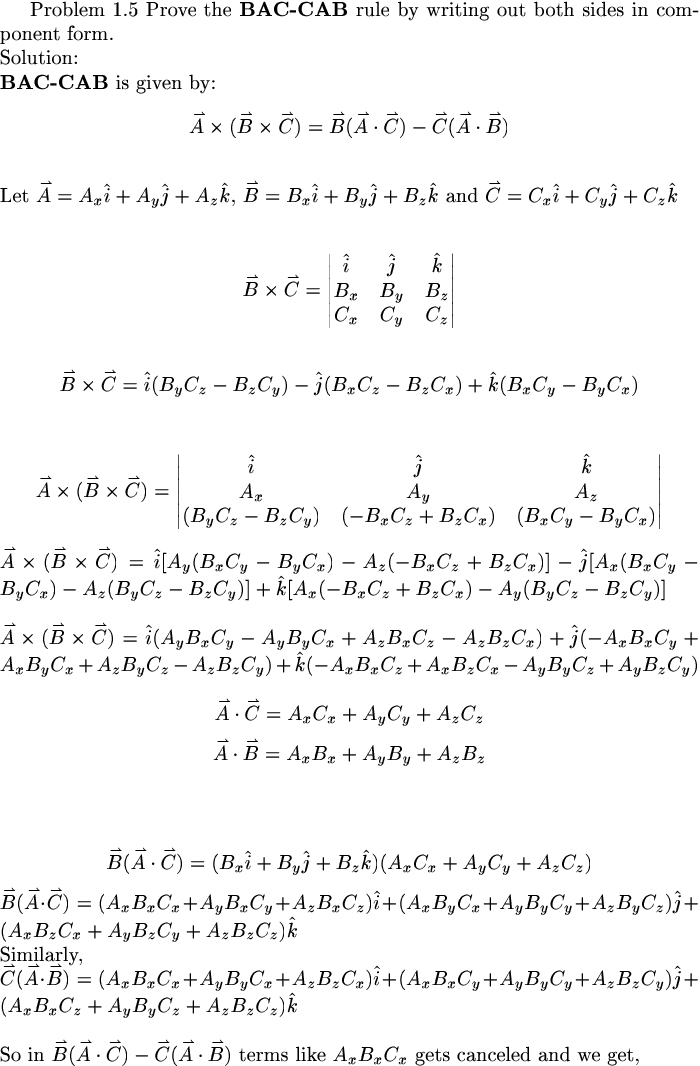List of Questions and link to solutions
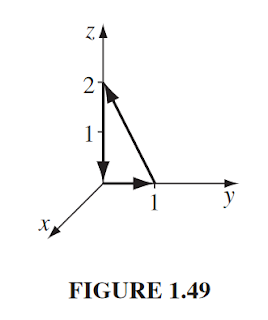
Chapter 1: Vector Analysis Problem 1.1: Using the definitions in Eqs. 1.1 and 1.4, and appropriate diagrams, show that the dot product and cross product are distributive, a) when the three vectors are co-planar. b) in the general case. Solution Problem 1.2 Is the cross product associative? $$(\vec{A}\times \vec{B}) \times \vec{C} \overset{?}{=} \vec{A}\times (\vec{B} \times \vec{C})$$ If so, prove it; if not, provide a counterexample (the simpler the better). Solution Problem 1.3 Find the angle between the body diagonals of a cube. Solution Problem 1.4 Use the cross product to find the components of the unit vector $\hat{n}$ perpendicular to the shaded plane in Fig. 1.11. Solution Problem 1.5 Prove the BAC-CAB rule by writing out both sides in component form. Solution Problem 1.6 Prove that $$[\vec{A}\times (\vec{B}\times \vec{C})]+[\vec{B}\times (\vec{C}\times \vec{A})]+[\vec{C}\times (\vec{A}\times \vec{B})] = 0$$ Under what conditions does $\vec{A}\times (\vec{B}\times \v